Mathematics is one of those classes that you sit through hoping that in the end something is applicable out of it. For mathematician Axel Wagner, it is an important tool to 100% his game of Legend of Zelda: Breath of th Wild.

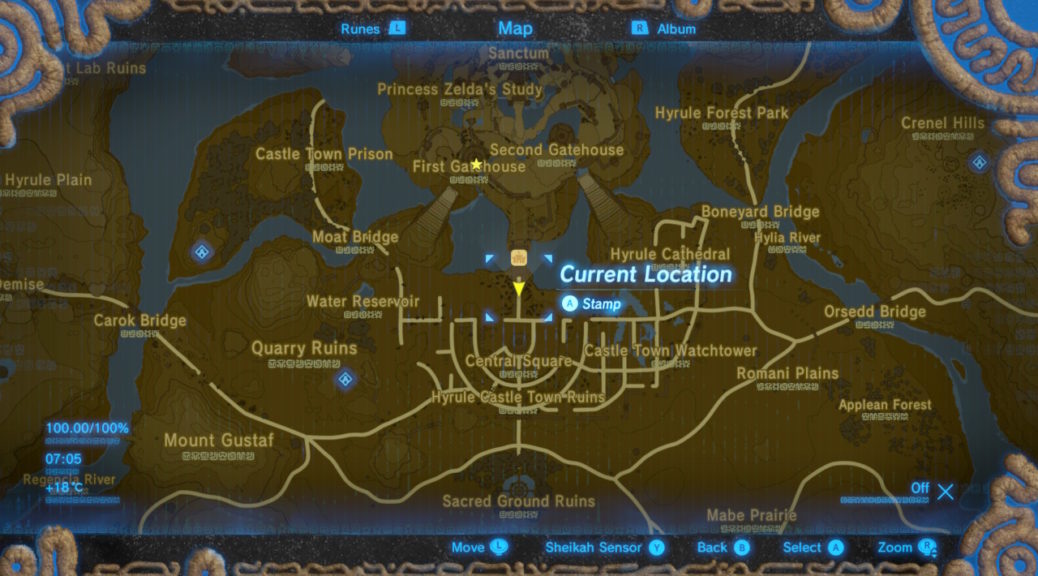
For those who have played the game, you would have known that there are a few factors that account for the game completion statistics. From the easily attainable Shrines to the tedious Korok Seeds, perhaps the hardest of them all is visiting every landmark and location. That is where Wagner’s solution come in, more specifically that is where his application of Hilbert’s curve come in.

In his words:

I needed a more systematic approach. I started to instead go through an alphabetical list of locations, looking up each on the map and see if I already had it mapped. But that got old really quickly. Alphabetical just wasn’t a great way to organize these; I wanted a list that I could systematically check. But I didn’t want it alphabetically but geographically. I didn’t want to have to jump around the map to try and find the next one. Which is when I realized that this would be the perfect application for a Hilbert curve.

If you don’t know (though you should really just read the Wikipedia Article), the Hilbert curve is a space filling fractal curve, that is a continuous bijective map from the real number line to the plane. It is iteratively defined as the limit of finite curves that get denser and denser. One of the most interesting properties of the curve and its finite approximations is that points that are close on the real number line get mapped to points that are close in the plane. So if we could extract all locations from the online map, figure out for each what real number gets mapped to that point and order the locations by those numbers, we’d get a list of locations where neighbors in the list are close to each other on the map. Presumably, that would make for easy checking of the list: The next location should be pretty much neighbouring the previous one and if I can’t find a location nearby, chances are that I didn’t visit it yet (and I can then look it up specifically).

What this means in layman terms is that Wagner used Hilbert Curves to make it quicker to find his way across locations without jumping across the map tediously again and again.

There is no easier way to explain the discrete math topic without going to in-depth but you can read up more on the Wikipedia page for Hilbert Curve (link), as well as, Wagner’s method of application (link).

For the rest of us who still struggle to understand, don’t give up, we may need a longer time, but we’ll get there!